En esta sección, las tasas de infección simuladas y las actividades económicas obtenidas del modelo BTH-SEIRS se comparan con datos del mundo real de España, que se vio afectada por la pandemia de COVID-19. Más específicamente, nuestro objetivo es reproducir el proxy basado en el turismo generado a partir de los datos de Eurostat como se detalla en la sección anterior, haciendo solo algunas comparaciones con los datos de tasas de infección de nuestro universo de datos.2. Los parámetros epidemiológicos del modelo se determinan según nuestro trabajo anterior, mientras que los parámetros socioeconómicos se tratan como libres. Nuestra tarea entonces es encontrar un conjunto de parámetros sociales y económicos tales que el indicador de la actividad económica se reproduzca lo más fielmente posible. Esta sección contiene dos subsecciones, la primera trata de los detalles del proceso de encontrar valores de parámetros apropiados y la segunda se refiere a la comparación real de datos simulados y reales.
Instalación del modelo
El modelo BTH-SEIRS contiene criterios epidemiológicos y sociales. Los parámetros anteriores se establecen según nuestra publicación anterior.11, teniendo en cuenta la virulencia de las diferentes variantes del virus y la tasa de inmunización de la población. Este trabajo busca comprender la dinámica socioeconómica de la población en respuesta a la epidemia y, por lo tanto, no intentamos replicar curvas de recuento de casos. Además, hay que tener en cuenta que estas curvas de casos diarios sirven de guía para determinar el número aproximado de casos pero pueden ser incompletas o inexactas, ya que no todas las personas que han contraído la enfermedad se han realizado la prueba, o si lo han hecho, generalmente lo hacen. No lo han reportado, el mismo día se enfermaron. Teniendo esto en cuenta, utilizamos únicamente casos diarios obtenidos del modelo SEIRS como fuente de información para los mecanismos de toma de decisiones. El modelo BTH debería reflejar datos económicos aproximados de España. Para ello tomamos en cuenta las siguientes consideraciones.
El modelo BTH contiene seis parámetros o ponderaciones que determinan la actitud de los agentes y autoridades de la población hacia la tasa de infección, la economía y las restricciones (ver Material complementario). Para elegir los pesos de las autoridades se tuvieron en cuenta tres periodos. Durante el primer período (día 0-249), hubo gran preocupación por la tasa de infección, lo que llevó a que se tomaran medidas restrictivas y se diera una prioridad relativamente menor a la economía. En el segundo período (día 250-499), si bien se mantuvieron la mayoría de las recomendaciones, el gobierno comenzó a darle mayor importancia a la economía. Finalmente, en el tercer período (día 500-1000), una vez vacunado el 70% de la población, la tasa de infección se volvió menos alarmante y se redujeron las restricciones y aportes económicos realizados por el gobierno para combatir la epidemia. (Ver Figura 4C-E). Las fechas de estos períodos fueron elegidas teniendo en cuenta la variación de las curvas que se muestran en la Figura 4A, B. La Figura 4A muestra el índice de rigurosidad.30Es una medida de cuán estricta es la respuesta del gobierno a la pandemia. Este índice va de 0 a 100, siendo 100 el más restrictivo para medidas como cierre de escuelas y lugares de trabajo y restricciones de movimiento, entre otras. La Figura 4 muestra el porcentaje de la población vacunada con dos dosis en azul y el porcentaje de la población que recibió vacunas de refuerzo en naranja (datos extraídos de Our World in Data2(Todos los pesos de los agentes de la Autoridad)\(W^X_i\), \(W^Y_i\)Y \(W^Z_i\)) se consideraron negativos para cumplir con los supuestos de voltaje mínimo. Similarmente, \(w^x_i\) Y \(w^y_i\) Se consideró negativo. Sin embargo, se ha demostrado \(w^c_i\) Debe ser positivo, considerando que la población en general estaba inicialmente dispuesta a cumplir con las restricciones impuestas por los agentes del poder.
En general, los agentes poblacionales tuvieron un cambio gradual de comportamiento. Al comienzo de la epidemia, la falta de conocimiento y la necesidad de protegerse contra la enfermedad llevaron a un mayor nivel de cumplimiento. Sin embargo, con el tiempo se observó que la población se volvió menos dispuesta a cumplir con las restricciones y con la llegada de las vacunas buscaron restablecer la actividad económica. Este cambio gradual se refleja en la modificación del modelo, que divide el tiempo en 6 períodos elegidos en función de las diferencias en las curvas de las Figuras 4A y B. El primer período vio restricciones estrictas y un alto cumplimiento (hasta 180 días). El segundo período (181-250 días), que coincidió con el verano, vio una disminución en el cumplimiento de la población. El tercer período (251-500 días) se caracterizó por la llegada de las vacunas y el cansancio de las restricciones, lo que provocó un menor cumplimiento de la población y poco interés en reducir su economía. En el cuarto período (501-600 días) se aceleró la vacunación, lo que estimuló a la población a volver a su vida normal y mejorar su situación económica. En el quinto período (601-800 días) se introdujeron vacunas de refuerzo, mientras que en el sexto período la mayoría de las personas estaban completamente vacunadas con vacunas de refuerzo, lo que redujo significativamente el interés de la población por la epidemia y, por tanto, su voluntad de cumplir con las restricciones o tomar medidas económicas. Contribuciones. El comportamiento antes mencionado en estos períodos se reflejó en la caída del valor absoluto de los docentes \(w^y_i\)Y \(w^c_i\) (Ver Figura 4G,H) y un aumento en el valor absoluto de \(w^x_i\) Factor.
Información utilizada para ayudar a elegir fechas para cambiar pesos y valores procesados. (a) Mostramos el índice de rigurosidad.30 Como medida de la severidad de las medidas tomadas por el gobierno. (B) Muestra la tasa de vacunación. La línea azul representa la vacunación total. La línea naranja representa refuerzos de vacunas.2. En ambas figuras, las líneas verticales discontinuas representan los momentos que elegimos para cambiar los pesos en el modelo. (C–h) son los pesos ajustados para cada período. Se observa que los parámetros modificados por los funcionarios de la autoridad indican un cambio en el tiempo en la posición hacia la reducción de las actividades económicas y hacia la epidemia. En el caso de los agentes poblacionales se observó una disminución en el cumplimiento de las recomendaciones y un cambio de actitud hacia la limitación de sus actividades económicas con el fin de reducir la tasa de contagios.
Vale la pena señalar que, como hemos demostrado17El modelo BTH-SEIRS puede arrojar resultados similares utilizando diferentes conjuntos de parámetros de valor, especialmente cuando las proporciones de los parámetros son las mismas. En este estudio, adoptamos la opinión de que con el tiempo los agentes se vuelven más vacilantes ante los esfuerzos de mitigación de la pandemia, pero también podríamos haber obtenido resultados similares asumiendo que las actitudes de los agentes con el tiempo tienden hacia la normalidad, es decir, \(W^X_i=W^Y_i=w^x_i=w^y_i=0\)Y \(W^Z_i\), \(w^c_i\) Con valores que se consideran normales para una sociedad típica.
Compara simulaciones numéricas con datos reales.
Para comparar los resultados del modelo BTH-SEIRS con datos de tasas de infección del mundo real y un sustituto económico basado en el turismo, realizamos una gran cantidad de simulaciones utilizando el modelo y calculamos las medias de las tasas de infección y la actividad económica. Como estimación del error también evaluamos \(90\%\) Rango cuantitativo calculado por eliminación \(5\%\) Tanto para los valores más altos como para los más bajos producidos por las simulaciones en cada paso de tiempo por separado. Este tipo de estimación del error se ha utilizado en contextos epidemiológicos y su uso es apropiado aquí dada la naturaleza altamente estocástica del modelo. Como se mencionó anteriormente, tratamos los parámetros SEIRS (\(\lambda\), \(\épsilon\)etc.) como constantes ya definidas por trabajos anteriores sobre el modelo SEIRS puro (ver, por ejemplo8,9,11), mientras que tratamos los parámetros de valor que rigen las actividades de los agentes como modificables. Nuestro objetivo entonces era encontrar valores numéricos de los parámetros que se reprodujeran mejor con datos del mundo real.
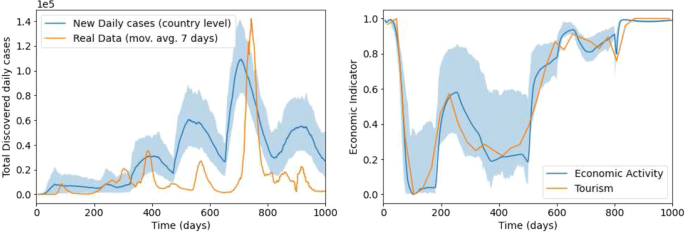
Comparación de la tasa de infección modelada con la tasa real (panel izquierdo) y la actividad económica modelada con datos de turismo de Eurostat (panel derecho). El modelo se ejecutó 100 veces para obtener el promedio mostrado por la curva azul. Aparece una sombra azul \(90\%\) Rango cuantitativo.
El mejor ajuste de los datos modelados a las verdaderas tasas de infección y niveles de actividad económica que podemos encontrar se puede ver en la Figura 5. La sombra azul representa la región que contiene \(90\%\) de repeticiones. Por conveniencia, hemos priorizado la frecuencia de los datos de actividad económica, que se puede ver claramente en el gráfico. Elegimos este enfoque principalmente porque en este trabajo queríamos centrarnos en el aspecto social del modelo BTH-SEIRS y, en segundo lugar, porque artículos anteriores sobre el modelo SEIRS han demostrado que el modelo SEIRS puro puede replicar las tasas de infección con bastante precisión. Como resultado, las tasas de infección que obtenemos del modelo no suelen coincidir cuantitativamente con las tasas de infección del mundo real, especialmente en la segunda mitad de la línea de tiempo, pero se ha descubierto que al menos los picos de las olas de infección ocurren aproximadamente en los mismos momentos. . Esto es de esperar, especialmente durante el reciente período de la pandemia, ya que no todos los casos de infección supuestos por el modelo fueron realmente reportados. Por el contrario, pudimos reproducir la actividad económica razonablemente bien, excepto por el verdadero pico global de alrededor de 230 días.
Como puede verse en la posición de la curva de actividad económica promedio simulada en relación con la tangente en la Figura 5, la distribución de las actividades económicas simuladas es asimétrica. En la mayoría de los intervalos de tiempo, la actividad económica promedio simulada se encuentra en la parte inferior de la región sombreada, lo que indica una distribución densa en la que la mayoría de las simulaciones se encuentran en la parte inferior de la sombra, mientras que también hay una gran cantidad de valores atípicos en la parte superior de la sombra. .

«Solucionador de problemas. Gurú de los zombis. Entusiasta de Internet. Defensor de los viajes sin disculpas. Organizador. Lector. Aficionado al alcohol».

